Zastanawiasz się, jak łatwo przekształcić długie ciągi zer i jedynek w bardziej zrozumiałe dane? Konwersja z systemu binarnego na szesnastkowy to kluczowa umiejętność w świecie informatyki, która znacząco upraszcza pracę z kodem. Ten artykuł przeprowadzi Cię krok po kroku przez cały proces, wyjaśniając jego podstawy i pokazując praktyczne zastosowania. Jako Nikodem Adamczyk, postaram się przekazać Ci tę wiedzę w sposób jak najbardziej przystępny i praktyczny, bazując na moim doświadczeniu.
Szybka ścieżka: Konwersja binarna na szesnastkową w kilku krokach
- System szesnastkowy (heksadecymalny) jest zwieńczeniem systemu binarnego, ponieważ każda cyfra szesnastkowa odpowiada dokładnie czterem bitom (2^4 = 16).
- Kluczową metodą konwersji jest grupowanie bitów liczby binarnej w pakiety po cztery, zaczynając od prawej strony.
- Niepełne grupy bitów na początku liczby binarnej należy uzupełnić zerami wiodącymi (z lewej strony).
- Każdą 4-bitową grupę zamienia się na odpowiadającą jej cyfrę szesnastkową (0-9, A-F) za pomocą tabeli konwersji.
- System szesnastkowy jest szeroko stosowany w informatyce, m.in. do definiowania kolorów (HTML/CSS), adresowania pamięci czy reprezentacji adresów MAC.
- Konwersja w drugą stronę (szesnastkowy na binarny) jest równie prosta i polega na rozpisaniu każdej cyfry szesnastkowej na jej 4-bitowy odpowiednik.
Od chaosu zer i jedynek do elegancji: dlaczego warto zamieniać system binarny na szesnastkowy?
W świecie cyfrowym, gdzie wszystko sprowadza się do zer i jedynek, umiejętność efektywnego zarządzania tymi danymi jest na wagę złota. Konwersja na system szesnastkowy to nie tylko sztuczka matematyczna, ale przede wszystkim praktyczne narzędzie, które znacząco ułatwia życie programistom i inżynierom.Po co skracać długie ciągi binarne? Praktyczny powód
Wyobraź sobie, że musisz zapamiętać, odczytać lub analizować długi ciąg bitów, na przykład 11010110111001010011. To jest po prostu męczące i bardzo podatne na błędy! Ludzki umysł nie jest przystosowany do przetwarzania tak wielu identycznych symboli w długich sekwencjach. System binarny, choć fundamentalny dla działania komputerów, jest dla nas, ludzi, niezwykle nieczytelny i trudny do zapamiętania. Właśnie dlatego potrzebujemy pośrednika systemu szesnastkowego.
System szesnastkowy oferuje znacznie bardziej zwartą i czytelną reprezentację tych samych danych. Zamiast dwudziestu cyfr binarnych, moglibyśmy mieć zaledwie pięć cyfr szesnastkowych. To ogromna różnica w czytelności, która znacząco ułatwia pracę z kodem, adresami pamięci czy wartościami kolorów. Z mojego doświadczenia mogę powiedzieć, że opanowanie tej konwersji to podstawa efektywnej pracy w wielu obszarach informatyki.
Zrozumieć fundamenty: Jaki jest związek między liczbą 2 a 16?
Kluczem do zrozumienia, dlaczego konwersja binarna na szesnastkową jest tak prosta i intuicyjna, leży w matematycznej relacji między podstawami tych systemów. System binarny ma podstawę 2, a szesnastkowy podstawę 16. Jak się okazuje, 16 to nic innego jak 2 podniesione do potęgi 4 (2^4 = 16). Ta prosta zależność jest absolutnie kluczowa!
Oznacza to, że każda jedna cyfra szesnastkowa może reprezentować dokładnie cztery cyfry binarne, czyli cztery bity. Dzięki temu możemy "pakować" bity w grupy po cztery, a następnie każdą taką grupę zamienić na pojedynczą, łatwiejszą do zarządzania cyfrę szesnastkową. To właśnie ta zależność sprawia, że konwersja jest tak bezpośrednia i nie wymaga skomplikowanych obliczeń, jak w przypadku konwersji na system dziesiętny.

Klucz do konwersji: Niezawodna metoda grupowania po 4 bity
Skoro rozumiemy już, dlaczego system szesnastkowy jest tak użyteczny i jaka jest jego relacja z systemem binarnym, przejdźmy do konkretów. Proces konwersji jest metodyczny i, co najważniejsze, bardzo prosty do opanowania. Wystarczy zapamiętać trzy proste kroki.
Krok 1: Jak poprawnie grupować bity? Zasada prawej strony
Pierwszym i absolutnie fundamentalnym krokiem jest podzielenie liczby binarnej na grupy po cztery bity. Tutaj pojawia się bardzo ważna zasada: grupowanie musi zawsze rozpoczynać się od prawej strony liczby, czyli od najmniej znaczącego bitu. Dlaczego? Ponieważ to gwarantuje, że każda grupa zachowa swoją prawidłową wartość pozycyjną. Jeśli zaczniesz grupować od lewej, zmienisz znaczenie bitów i otrzymasz błędny wynik. Pamiętaj, że każdy bit ma swoją "wagę" w liczbie, a ta waga rośnie od prawej do lewej.
Krok 2: Co zrobić, gdy na początku zostanie „samotna” grupa bitów? Sztuczka z dopełnianiem zerami
Często zdarza się, że liczba bitów w ciągu binarnym nie jest idealną wielokrotnością czterech. Co wtedy? Spokojnie, to żaden problem! Jeśli po pogrupowaniu od prawej strony, skrajna lewa grupa bitów nie zawiera pełnych czterech cyfr (np. ma tylko jeden, dwa lub trzy bity), należy ją uzupełnić zerami wiodącymi (z lewej strony), aby uzyskać pełną czwórkę. Te zera wiodące nie zmieniają wartości liczby, ale są niezbędne do prawidłowej konwersji na cyfrę szesnastkową.
Na przykład ciąg 101101 dzieli się na 10 i 1101. Pierwszą grupę, 10, uzupełniamy do 0010. Teraz mamy dwie pełne grupy po cztery bity: 0010 i 1101. To prosta, ale kluczowa sztuczka, którą często widzę, że początkujący pomijają.
Krok 3: Zamiana grup na cyfry: Twoja ściągawka z tabelą konwersji
Ostatni krok to zamiana każdej 4-bitowej grupy na odpowiadającą jej pojedynczą cyfrę szesnastkową. System szesnastkowy używa cyfr od 0 do 9 oraz liter od A do F, gdzie A reprezentuje wartość dziesiętną 10, B to 11, i tak dalej, aż do F, które oznacza 15. Poniższa tabela to Twoja "ściągawka", którą warto mieć pod ręką, dopóki nie opanujesz konwersji na pamięć. Jest to serce całej operacji!
| Grupa binarna (4 bity) | Cyfra szesnastkowa |
|---|---|
| 0000 | 0 |
| 0001 | 1 |
| 0010 | 2 |
| 0011 | 3 |
| 0100 | 4 |
| 0101 | 5 |
| 0110 | 6 |
| 0111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | A |
| 1011 | B |
| 1100 | C |
| 1101 | D |
| 1110 | E |
| 1111 | F |
Zobacz to w akcji: Przykłady, które rozwieją każdą wątpliwość
Teoria to jedno, ale praktyka to drugie. Przyjrzyjmy się kilku przykładom, które ugruntują Twoje zrozumienie procesu konwersji. Zobaczysz, że to naprawdę proste!
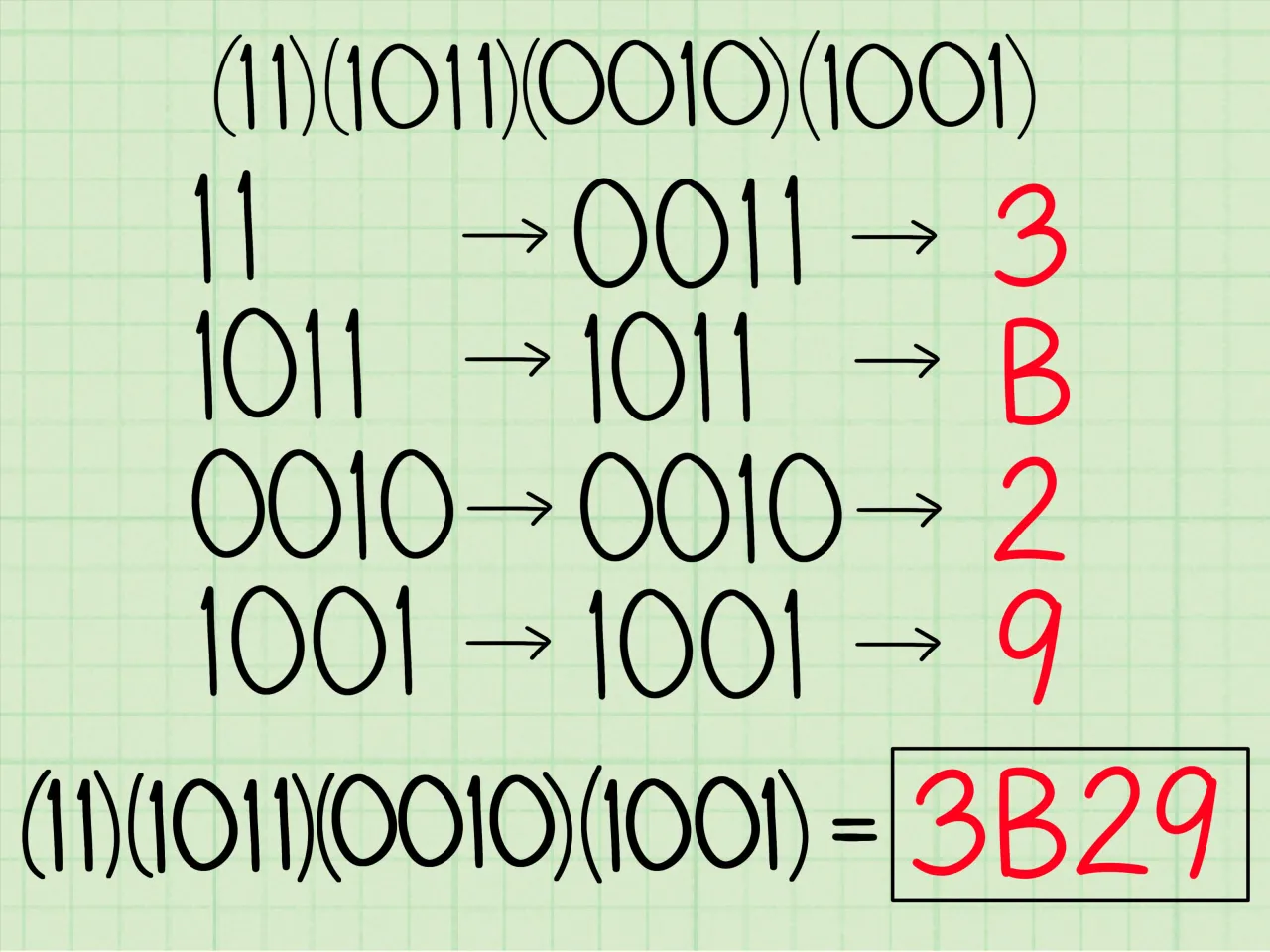
Przykład podstawowy: Konwersja liczby 11011010 krok po kroku
Weźmy liczbę binarną 11011010.
- Najpierw dzielimy liczbę na grupy po cztery bity, zaczynając od prawej strony:
1101 1010. W tym przypadku liczba bitów jest wielokrotnością czterech, więc nie musimy nic uzupełniać. - Następnie, używając naszej tabeli konwersji, zamieniamy każdą grupę na jej szesnastkowy odpowiednik:
-
1101toD -
1010toA
-
- Ostateczny wynik to po prostu połączenie tych cyfr:
DA. Proste, prawda?
Przykład dla dociekliwych: Jak zamienić liczbę 101110, która nie dzieli się przez 4?
Teraz przykład, który uwzględnia uzupełnianie zerami. Przekonwertujmy liczbę binarną 101110.
- Grupujemy od prawej strony:
10 1110. Zauważ, że lewa grupa (10) ma tylko dwa bity. - Wyjaśniamy konieczność uzupełnienia lewej grupy zerami wiodącymi, aby miała cztery bity:
0010 1110. - Zamieniamy grupy na szesnastkowe odpowiedniki, korzystając z tabeli:
-
0010to2 -
1110toE
-
- Ostateczny wynik to:
2E. Widzisz, uzupełnianie zerami nie jest takie straszne!
Przykład zaawansowany: Praca z dłuższą liczbą binarną
Spróbujmy z dłuższą liczbą: 1111000010101111. W tym przypadku liczba bitów jest wielokrotnością czterech, więc będzie to nieco prostsze niż poprzedni przykład, ale pokaże, jak radzić sobie z większymi wartościami.
- Dzielimy na grupy po cztery bity, zaczynając od prawej:
1111 0000 1010 1111. - Zamieniamy każdą grupę na jej szesnastkowy odpowiednik:
-
1111toF -
0000to0 -
1010toA -
1111toF
-
- Ostateczny wynik to:
F0AF. Jak widać, nawet długie ciągi binarne stają się bardzo czytelne w systemie szesnastkowym.
Najczęstsze pułapki i jak ich unikać: błędy, których już nie popełnisz
W każdym nowym zagadnieniu zdarzają się typowe błędy. Chcę Cię przed nimi przestrzec, abyś mógł od razu pracować efektywnie i bez frustracji. Z mojego doświadczenia wynika, że te trzy pomyłki są najczęstsze.
Pomyłka nr 1: Grupowanie od złej strony
To chyba najczęstszy błąd, jaki widzę. Niektórzy początkujący próbują grupować bity od lewej strony (od najbardziej znaczącego bitu). Pamiętaj, że zawsze musisz zaczynać grupowanie od prawej strony. Dlaczego to takie ważne? Ponieważ każdy bit ma swoją "wagę" w liczbie. Bit na skrajnej prawej stronie (najmniej znaczący bit) ma wagę 2^0, kolejny 2^1 i tak dalej. Jeśli zaczniesz grupować od lewej, to tak, jakbyś zmieniał kolejność cyfr w liczbie dziesiętnej wynik będzie zupełnie inny i oczywiście błędny. Zawsze myśl o tym, jak o odczytywaniu liczby od końca.
Pomyłka nr 2: Zapominanie o literach A-F
System szesnastkowy to nie tylko cyfry od 0 do 9! Bardzo łatwo zapomnieć, że używa on również liter A, B, C, D, E, F do reprezentowania wartości dziesiętnych od 10 do 15. Często widzę, jak ktoś zamienia 1010 na "10" zamiast na "A". To jest błąd! Pamiętaj, że każda grupa czterech bitów ma zostać zamieniona na pojedynczą cyfrę szesnastkową. Jeśli użyjesz "10", to tak, jakbyś miał dwie cyfry szesnastkowe (1 i 0), co całkowicie zmienia wartość. Zawsze odwołuj się do tabeli konwersji, dopóki nie będziesz pewien.
Pomyłka nr 3: Nieprawidłowe uzupełnianie zerami
Uzupełnianie zerami jest kluczowe, ale musi być wykonane prawidłowo. Zera dodajemy zawsze na lewo od najbardziej znaczącej grupy bitów, czyli na samym początku liczby. Nigdy nie dodawaj zer na końcu liczby binarnej, ponieważ to zmieni jej wartość! Na przykład, 101 to 5 dziesiętnie, a 1010 to 10 dziesiętnie. Dodanie zera na końcu zmienia wartość. Zera wiodące (np. 00101) nie zmieniają wartości (nadal jest to 5), ale są niezbędne do prawidłowego grupowania. Upewnij się, że dodajesz je tylko wtedy, gdy lewa grupa jest niepełna i tylko z lewej strony.
Gdzie w praktyce spotkasz system szesnastkowy? Informatyka w pigułce
Być może zastanawiasz się, po co w ogóle zawracać sobie głowę tymi konwersjami. Otóż system szesnastkowy jest wszechobecny w informatyce! Zrozumienie go to jak nauka języka, którym "mówią" komputery i programiści. Pozwól, że pokażę Ci kilka kluczowych zastosowań, które na pewno spotkasz w swojej przygodzie z technologią.
Kolory na stronach WWW: jak zapisany jest Twój ulubiony odcień?
Jeśli kiedykolwiek edytowałeś kod HTML lub CSS, na pewno natknąłeś się na kody kolorów, takie jak #FFFFFF (biały) czy #000000 (czarny). To są właśnie kody szesnastkowe! Każdy kolor jest reprezentowany przez trzy pary cyfr szesnastkowych, gdzie każda para definiuje intensywność składowej czerwonej, zielonej i niebieskiej (model RGB). Na przykład, #FF0000 to czysta czerwień, ponieważ FF (czyli 255 dziesiętnie) oznacza maksymalną intensywność czerwieni, a 00 (0 dziesiętnie) oznacza brak zieleni i błękitu. Dzięki systemowi szesnastkowemu, programiści mogą w zwięzły i czytelny sposób określać miliardy odcieni.
Adresy pamięci i debugowanie: język komputera
W programowaniu niskopoziomowym, na przykład podczas pracy z asemblerem, czy też w trakcie debugowania aplikacji, programiści bardzo często używają systemu szesnastkowego do reprezentowania adresów pamięci. Zamiast długich ciągów binarnych, które byłyby nieczytelne, adresy takie jak 0x7FFC3C78 są znacznie łatwiejsze do odczytania i zarządzania. Prefiks 0x często wskazuje, że dana liczba jest zapisana w systemie szesnastkowym. Pozwala to na szybkie odwoływanie się do konkretnych lokacji w pamięci, co jest nieocenione przy analizie działania programów i poszukiwaniu błędów.
Przeczytaj również: Binarny na dziesiętny krok po kroku: Opanuj język komputerów!
Unikalny identyfikator Twojej karty sieciowej: adres MAC
Każde urządzenie sieciowe, takie jak karta sieciowa w Twoim komputerze czy smartfonie, posiada unikalny adres sprzętowy zwany adresem MAC (Media Access Control). Adresy te są standardowo zapisywane w formacie szesnastkowym, na przykład 00:1A:2B:3C:4D:5E. Jest to 48-bitowy identyfikator, który w systemie binarnym byłby koszmarnie długi. Dzięki zapisowi szesnastkowemu, adres MAC jest czytelny, łatwy do skopiowania i zarządzania, co jest kluczowe w konfiguracji sieci i rozwiązywaniu problemów z łącznością.
A co w drugą stronę? Błyskawiczna konwersja z systemu szesnastkowego na binarny
Na koniec mam dla Ciebie dobrą wiadomość: proces konwersji z systemu szesnastkowego na binarny jest dokładnym przeciwieństwem tego, co właśnie omówiliśmy, i jest równie prosty! Wystarczy wziąć każdą cyfrę szesnastkową i zamienić ją na jej 4-bitowy odpowiednik binarny, korzystając z tej samej tabeli konwersji, którą poznałeś. Na przykład, jeśli masz liczbę szesnastkową 2E, zamieniasz 2 na 0010, a E na 1110, otrzymując 00101110. To intuicyjne i szybkie, co tylko potwierdza, jak spójne i użyteczne są te dwa systemy w informatyce.

